실험 목적
증발은 액체의 분자가 액체의 표면을 이탈하는 것이며 이는 상태변화의 한 과정이다. 이 실험에서는 물이 증발할 때 이로 인한 증기압을 구하고, 증발열을 구한다.
실험 이론 및 원리
증발은 액체가 개방된 용기에서 완전히 없어지는 것을 의미하며 이는 강한 분자간의 인력을 극복하는 것으로써 에너지를 소모하는 흡열반응이다. 이처럼 1기압의 압력에서 물이 증발하는데 필요한 에너지를 증발열이라고 한다. 온도에 의한 증기압의 관계는 기체를 이상기체로 가정할 때 다음의 Clausius-Clapeyron식에 의해 표시되어진다.
실험 기구 및 시약
1. 실험 기구
10㎖ 메스실린더, 1 L 톨비커, 온도계, 30㎝ 눈금자, 스탠드, 기압계, hot plate
2. 실험 시약
증류수, 얼음
실험 방법
1. 실험 과정
1) 10㎖ 눈금실린더에 물을 2/3정도 채우고, 물을 채운 비커에 거꾸로 넣는다.
2) 비커에 온도계와 눈금자를 함께 넣는다.
3) 눈금실린더 위 부분까지 비커의 물이 차게 한다.
4) 80℃까지 가열한 후 식힌다.
5) 65℃, 60℃, 55℃, 3℃에서 물의 온도, 공기층 사이의 높이, 기체의 부피를 측정한다.
실험 결과
1. 결과 분석
1) 실험 그래프
2) 실험 데이터
온도(K) | 측정된 부피(㎖) | 보정된 부피(㎖) | 공기압 | 물의 증기압 |
338 | 8.5 | 8.3 | 579.09(torr) | 191.20(torr) |
333 | 7.8 | 7.6 | 623.07(torr) | 146.78(torr) |
328 | 7.38 | 7.18 | 649.61(torr) | 120.06(torr) |
5℃ 이하의 결과 | ||||
276 | 5.3 | 5.1 | 769.56(torr) | 0 |
T(K) | 338 | 333 | 328 |
1/T(10-3K-1) | 0.00296 | 0.00300 | 0.00305 |
lnPH2O | 5.253349 | 4.988924 | 4.787961 |
3) 이론값
T(K) | 338 | 333 | 328 |
물의 증기압(PH2O) | 187.5(torr) | 149.4(torr) | 118(torr) |
lnPH2O | 5.233779 | 5.006627 | 4.77068 |
직선의 기울기(S) = -5155
물의 증발열 실험값 = R×S = -5155×8.3145J/㏖ = -42861J/㏖
물의 증발열 이론값 = -5134×8.3145J/㏖ = -42687J/㏖
2. 계산 과정
1) 0℃일 때,
공기압 = 대기압 + ρgh (물의 증기압 = 0)
대기압=102,071.61 Pa
ρgh = (999.9kg/㎥)×(9.8m/s2)×(0.054m) = 529.14Pa
(kg/㎥=g/L)
Pa=N/㎡
N=㎏m/s2
공기압 = 102,071.61 + 529.14 = 102,600.76Pa
공기압=nRT/V
n=PV/RT
n = {102,600.76Pa×(1N/㎡/Pa)×(5.1×10-6㎥)}/{8.315J/㏖K×(276)K} = 2.2802×10-4㏖
2) 65℃일 때,
물의 증기압(PH2O) = 대기압 + ρgh - 공기압
대기압 = 102,071.61 Pa
ρgh = (980.59kg/㎥)×(9.8m/s2)×(0.068m) = 653.47
공기압 = {2.2802×10-4㏖×(8.3145J/㏖K)×(338K)}/{8.3×10-6㎥} = 77205.40
물의 증기압(PH2O) = 102,071.61 + 653.47 - 77205.40 = 25519.06Pa = 191.2055mmHg
3) 60℃일 때,
물의 증기압(PH2O) = 대기압 + ρgh - 공기압
대기압 = 102,071.61 Pa
ρgh = (983.24kg/㎥)×(9.8m/s2)×(0.061m) = 587.78
공기압 = {2.2802×10-4㏖×(8.3145J/㏖K)×(333K)}/{7.6×10-6㎥} = 83069.14
물의 증기압(PH2O) = 102,071.61 + 587.78 - 83069.14 = 19589.64Pa = 146.7784mmHg
4) 55℃일 때,
물의 증기압(PH2O)=대기압+ρgh-공기압
대기압 = 102,071.61 Pa
ρgh = (985.73kg/㎥)×(9.8m/s2)×(0.058m) = 560.29
공기압 = {2.2802×10-4㏖×(8.3145J/㏖K)×(328K)}/{7.18×10-6㎥} = 86608.09
물의 증기압(PH2O)=102,071.61+560.29-86608.09=16023.2Pa=120.0563mmHg
토의 사항
1. 실험 고찰
실험은 매우 성공적이었다. 물의 증발열(실험값)과 물의 증발열(이론치) 간의 차이가 매우 작았기 때문이다. 따라서 오차 분석은 생략하고, Clausius-Clapeyron식을 쓰는데 따른 가정들을 살펴보고, 그러한 가정이 왜 필요한 지 분석한다.
Clausius-Clapeyron식을 사용하기 위해 다음과 같은 가정이 필요하다.
1) 액체와 기체상 사이의 평형 상태
2) 증기는 이상기체 이다.
3) 액체의 몰부피는 증기의 몰부피에 비교해 무시할 수 있다.
4) 증발열은 온도에 무관하다.
① ul = ug
액체와 기체의 상평형 상태를 가정했기 때문에, 화학퍼텐셜(다성분계에서 각 성분의 1㏖에 할당되는 에너지)가 같다. 또한 화학퍼텐셜의 미소변화는 자유에너지에 몰수를 나눈 값과 같으므로,
② du = -SmdT + VmdP
①, ②에 의해
③ -Sm,ldT + Vm,ldP = -Sm,gdT + Vm,gdP
④ dP/dT = (Sm,g-Sm,l)/(Vm,g-Vm,l)
③번 가정에 의해
⑤ dP/dT = (Sm,vap)/(Vm,g)
상평형을 가정하였으므로, 등온, 등압, 가역 반응이다.
따라서 아래의 식이 성립한다.
⑥ ΔS = ΔHvap/T
⑤, ⑥에 의해
⑦ dP/d = ΔHvap/(T×Vm,g)
이상기체를 가정하였으므로 Vm,g는 RT/P이다. 따라서 아래의 식이 성립한다.
⑧ 1/P․dP/dT = ΔHvap/RT2
⑨ dx/x = dlnx
⑧, ⑨에 의해
⑩ dlnP/dT = ΔHvap/RT2
실험결과와 이론값를 비교했을 때, 가정들이 대부분 지켜졌다고 볼 수 있다. 그러나 증기가 이상기체가 아니므로 가정에 위배된 셈이지만, 오차가 매우 작았으므로, 이상기체에 거의 가까웠다고 볼 수 있다.
참고 문헌
1. 일반화학실험, 서울시립대학교 교양화학, 드림플러스, 2013


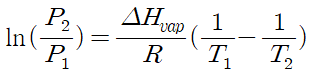


!&emoji=☕&slug=xFu35q9&button_colour=5F7FFF&font_colour=ffffff&font_family=Poppins&outline_colour=000000&coffee_colour=FFDD00)



![[일반생물학실험]온도와 pH가 효소작용에 미치는 영향 1부](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjdvNA5S925m8lScjFhJj-uy5SdCcaNFG1AuR_7BbQbDEoHBDEEkqfM64sipvro3RydmSO4_MS2794o2bJ0FCljQ31pcD5W39ZGOHROD7qKXLO1rlm2ZuBtbxJ9CZHSnsk2v1KSEsL4EGA/w680/%25EC%2598%25A8%25EB%258F%2584%25EC%2599%2580+pH%25EA%25B0%2580+%25ED%259A%25A8%25EC%2586%258C%25EC%259E%2591%25EC%259A%25A9%25EC%2597%2590+%25EB%25AF%25B8%25EC%25B9%2598%25EB%258A%2594+%25EC%2598%2581%25ED%2596%25A5.PNG)
![[일반생물학실험]여러 조건에 따른 효소 반응](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj4kaETe9N8j9q9-ClYy9V1kM2L9s5l19K6YoBOE0SB70BmssQXzVADvQijp1ieiQ9mIxcmCwz9e-YCQFVnXYR7m1vmfjTSs0ZNxCmBLG7wgzRBqiY1Kizx8YuhSdw-RDbs1PohokUd69c/w680/%25EC%2597%25AC%25EB%259F%25AC+%25EC%25A1%25B0%25EA%25B1%25B4%25EC%2597%2590+%25EB%2594%25B0%25EB%25A5%25B8+%25ED%259A%25A8%25EC%2586%258C+%25EB%25B0%2598%25EC%259D%2591.PNG)
![[일반생물학실험]항생제 감수성 검사 1부](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhwCJEjB_r2Ojsrn244q-fQmpHsDyUUfgWMUnsfhPKQeN2e7_u1pN_ZuwIdxPLVWS6LFywJUrDTYWJe2V6ZVVb1PtfyvX62Y15OxPfXoiaJkqVoSir3ZoFAmDpe5GcoMBmxEsJUKsSvWYc/w680/%25ED%2595%25AD%25EC%2583%259D%25EC%25A0%259C+%25EA%25B0%2590%25EC%2588%2598%25EC%2584%25B1+%25EA%25B2%2580%25EC%2582%25AC.PNG)
![[고분자공학실험]PMMA 중합 반응 - MMA, AIBN 정제와 PMMA Bulk 중합 1부](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj5hkRZhYWcXolP679_yO0kyP8_R-G9dlTqk5AGEdfsIq9M5K3DJc_tvpYck4x1kciBm2IWwFygrzfWH-HPzUjXiCHAFrjv9zeKYDxAl2tGNqgryyc3t9y4B9lQveS_coAqnmZw4pX4Hyo/w680/PMMA+%25EC%25A4%2591%25ED%2595%25A9+%25EB%25B0%2598%25EC%259D%2591.PNG)
![[일반화학실험]산화-환원 적정 : 비타민 C의 정량 1부](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEintFUW1pYHbKK8MPzki4vdqVMjTUEFFxPdZB1sTJQw13XSFZWqcN5w0x1AlyzfErlYYSgoNqBni4YGlpFC4ZeULK9VHbhfIXLiuZ3UWTl2oBRua7FE8UUQqtYEx3498FENAnlHlh0f8RFkT7Na8jveOtBtQ5UbY8jE80ZCwFoU_jqw_0Z6BofRYZF7/w680/%EC%82%B0%ED%99%94-%ED%99%98%EC%9B%90%20%EC%A0%81%EC%A0%95%20-%20%EB%B9%84%ED%83%80%EB%AF%BC%20C%EC%9D%98%20%EC%A0%95%EB%9F%89.PNG)
0 댓글