실험 목적
실험 이론 및 원리
Two straingauges, which are attached in a right-angled tetragon cantilever, are composing Wheatstone bridge and giving load through load shell. And then look for relation generating power through Wheatstone bridge and Load. The next we give load 0.5kgf each time and find strain. Also compare measured strain value and theory strain value then calculate the elastic modulus of materials. Applying loads more added value because of increasing strain, load and strain values are proportional. We can find out the principle of electrical resistance strain gauges and How to attach to the specimen.
2. 응력과 변형률 관계
1) σw : 사용응력(Working Stress) - 사용할 수 있는 응력 = 영구 변형 없이 구조물을 안전하게 사용할 수 있는 응력
2) σa : 허용응력(allow stress) - 사용응력으로 선정한 안전한 범위의 응력 = 사용응력의 상한응력
3) σu : 극한강도(최대응력)
응력의 관계 σw ≦ σa =σu/S 여기서, S:안전율
인장강도=최대하중/최초의 단면적(인장시험의 최대하중을 최초의 단면적으로 나눈값)
3. 푸와송비
푸와송비는 x방향으로 축 응력(인장, 압축)을 받을 때, y, z축으로(가로방향) 변형이 이루어지는데, 축 방향 변형에 따른 가로방향변형의 비의 상수 값을 푸와송비라고 하고, ν(nu)로 표시된다.
4. 외팔보에 걸리는 하중과 변형률
그림 2과 같이 고정단 으로부터 l떨어진 자유단에 하중 W가 걸릴 때 a만큼 떨어진 위치에 부착한 스트레인 게이지의 스트레인은 다음식 으로 계산된다.
 |
| 그림 2 외팔보의 치수 및 하중 |
σ = Eε
탄성계수 E를 알고 있는 재료의 외팔보에 대하여 스트레인을 계산할 수 있다. 실험으로 측정한 스트레인과 이론식으로 계산한 스트레인을 비교 검토할 수 있다. 만약 탄성계수를 모르고 있는 재료에 대하여 스트레인을 측정한다면 탄성계수 E를 계산해낼 수 있을 것이다.
 |
| 참고 - 하중을 받는 보 |
그림 3과 같이 길이 L인 외팔보 AB가 자유단에서 집중하중 P를 받을 때 처짐곡선의 방정식을 구해보자.
 |
그림 3 집중하중을 받는 외팔보 |
고정단을 좌표의 원점으로 잡으면 고정단에서 거리 X만큼 떨어진 임의 점에서의 굽힘모멘트는
M = -P(L-x)
이 되고 위식을 EIv″ = -M에 대입하면 미분방정식은 다음과 같이 된다.
EIv″ = P(L-x)
위식을 적분하면
적분상수 C1은 고정단에서 보의 처짐각이 0이라는 조건에서 구할 수 있다. 즉 v′(0)=0 이므로 C1=0이다. 따라서 위식은
위식을 다시 적분하면
가 된다. 고정단에서 보의 처짐이 0이라는 조건, 즉 v(0)=0인 경계조건을 이용하면 C2=0가 된다. 따라서 처짐곡선의 방정식은 다음과 같이 된다.
최대처짐은 자유단에서 일어나며 위식에 x=L을 대입함으로써 구할 수 있다.
저항선에 길이의 변화(스트레인)을 주면 저항이 달라진다. 이 성질을 이용하여 저항의 변화를 측정하여 스트레인을 알아내는 저항선 게이지가 스트레인 게이지이다. 즉 스트레인을 측정하고자 하는 물체의 표면에 스트레인 게이지를 부착하고 하중을 가하여 저항의 변화를 측정하면 스트레인을 구할 수 있다.
그림 4에서와 같이 길이 l, 단면적 A, 비저항 ρ인 균질한 금속서의 저항 R은
 | |
| 그림 4. 포일스트레인 게이지 개략도 |
로 표시된다.
이 금속선의 외부로부터 힘을 받아 스트레스와 스트레인이 발생하여 길이가 Δl, 단면적 ΔA, 비저항이 Δρ 만큼 변하고 전기저항이 ΔR만큼 변화했다고 하면 스트레인이 작은 범위에서는 다음 식이 성립한다.
여기서 v는 Poisson비이고 Δl/l은 저항의 스트레인 ε을 의미한다. 위의 식에 양면을 ε으로 나누면
가 되는데 여기서 G는 게이지율(gauge factor)로 정의된다. 위의 식에서 저항선의 저항변화율과 게이지율을 알면 스트레인을 구할 수 있음을 알 수 있다. 대부분 금속합금에서 게이지율은 -12에서 +6까지 변하며, 스트레인 게이지에 가장 많이 사용되는 Advance(Ni:45% Cu:55%)의 게이지율은 2.0부근이다. 게이지율은 각각의 스트레인 게이지마다 다르며 제조회사에서 온도보정곡선과 함께 소수점 이하 두 자리까지 제공하는 것이 보통이다.
7. 휘스톤 브리지(Wheatstone bridge)
스트레인 양이 미소하기 때문에 전기저항의 변화나 검류계의 전류가 아주 작은 양이다. 이것을 확대하는 방법으로서 4개의 스트레인 게이지를 그림과 같은 회로로 구성하고 검류계의 전류를 측정하면 4배의 출력을 얻을 수 있다. 이 회로를 휘스톤 브리지라고 하며 확대원리는 다음과 같다.
회로에서 다음 식을 만족하면 검류계 G에 전류가 흐르지 않는다.(기준 상태)
R1이 외력으로 인장되어 저항이 ΔR만큼 증가하면 D점의 전압은 ΔV만큼 증가하고 G에 전류가 흐른다. 또 R4가 압축되어 -ΔR만큼 변하면 D의 전압이 ΔV만큼 증가한다.
 |
| 그림 5. 휘스톤 브리지 |













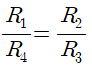
!&emoji=☕&slug=xFu35q9&button_colour=5F7FFF&font_colour=ffffff&font_family=Poppins&outline_colour=000000&coffee_colour=FFDD00)



![[일반생물학실험]온도와 pH가 효소작용에 미치는 영향 1부](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjdvNA5S925m8lScjFhJj-uy5SdCcaNFG1AuR_7BbQbDEoHBDEEkqfM64sipvro3RydmSO4_MS2794o2bJ0FCljQ31pcD5W39ZGOHROD7qKXLO1rlm2ZuBtbxJ9CZHSnsk2v1KSEsL4EGA/w680/%25EC%2598%25A8%25EB%258F%2584%25EC%2599%2580+pH%25EA%25B0%2580+%25ED%259A%25A8%25EC%2586%258C%25EC%259E%2591%25EC%259A%25A9%25EC%2597%2590+%25EB%25AF%25B8%25EC%25B9%2598%25EB%258A%2594+%25EC%2598%2581%25ED%2596%25A5.PNG)
![[일반생물학실험]여러 조건에 따른 효소 반응](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj4kaETe9N8j9q9-ClYy9V1kM2L9s5l19K6YoBOE0SB70BmssQXzVADvQijp1ieiQ9mIxcmCwz9e-YCQFVnXYR7m1vmfjTSs0ZNxCmBLG7wgzRBqiY1Kizx8YuhSdw-RDbs1PohokUd69c/w680/%25EC%2597%25AC%25EB%259F%25AC+%25EC%25A1%25B0%25EA%25B1%25B4%25EC%2597%2590+%25EB%2594%25B0%25EB%25A5%25B8+%25ED%259A%25A8%25EC%2586%258C+%25EB%25B0%2598%25EC%259D%2591.PNG)
![[일반생물학실험]항생제 감수성 검사 1부](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhwCJEjB_r2Ojsrn244q-fQmpHsDyUUfgWMUnsfhPKQeN2e7_u1pN_ZuwIdxPLVWS6LFywJUrDTYWJe2V6ZVVb1PtfyvX62Y15OxPfXoiaJkqVoSir3ZoFAmDpe5GcoMBmxEsJUKsSvWYc/w680/%25ED%2595%25AD%25EC%2583%259D%25EC%25A0%259C+%25EA%25B0%2590%25EC%2588%2598%25EC%2584%25B1+%25EA%25B2%2580%25EC%2582%25AC.PNG)
![[고분자공학실험]PMMA 중합 반응 - MMA, AIBN 정제와 PMMA Bulk 중합 1부](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj5hkRZhYWcXolP679_yO0kyP8_R-G9dlTqk5AGEdfsIq9M5K3DJc_tvpYck4x1kciBm2IWwFygrzfWH-HPzUjXiCHAFrjv9zeKYDxAl2tGNqgryyc3t9y4B9lQveS_coAqnmZw4pX4Hyo/w680/PMMA+%25EC%25A4%2591%25ED%2595%25A9+%25EB%25B0%2598%25EC%259D%2591.PNG)
![[일반화학실험]산화-환원 적정 : 비타민 C의 정량 1부](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEintFUW1pYHbKK8MPzki4vdqVMjTUEFFxPdZB1sTJQw13XSFZWqcN5w0x1AlyzfErlYYSgoNqBni4YGlpFC4ZeULK9VHbhfIXLiuZ3UWTl2oBRua7FE8UUQqtYEx3498FENAnlHlh0f8RFkT7Na8jveOtBtQ5UbY8jE80ZCwFoU_jqw_0Z6BofRYZF7/w680/%EC%82%B0%ED%99%94-%ED%99%98%EC%9B%90%20%EC%A0%81%EC%A0%95%20-%20%EB%B9%84%ED%83%80%EB%AF%BC%20C%EC%9D%98%20%EC%A0%95%EB%9F%89.PNG)
0 댓글