[기계공학실험]곡선보 응력 측정

실험 목적

스트레인게이지를 부착해 곡선 보에 하중을 가한 후 변형률을 측정한다. 측정한 변형률 에 훅의 법칙을 이용하여 응력을 계산하고 이론식과 비교해 본다.

실험 이론 및 원리

1. 스트레인게이지

Straingauge(변형률계 또는 응력계)라고 한다.

일반적인 전기적, 전자적 신호를 이용하여 공학적인 값을 측정하는 장비이다. 길이의 변화율을 진동현의 주파수(Hz) 코일의 저항 등을 이용하여 간접적으로 측정하는 장치이다.

 

2. 인장시험기

인장시험은 공업용 재료의 기계적 성질을 알기 위한 기본적인 시험으로써 일정한 속도로 반대방향으로 잡아당기는 힘에 대한 물질의 저항성을 측정하는 실험이다. 재료강도에 관한 기본적인 설계 정보를 얻기 위해 가장 널리 사용된다.

이를 통해 공업용 재료의 변형 과정과 응력의 변화를 조사하며, 재료의 항복강도, 인장강도, 연신율, 단면 수축율 등의 기계적인 특성과 탄성한계, 비례한계, 포아송비, 탄성계수의 물리적 특성을 구하는 것을 목적으로 한다.

 

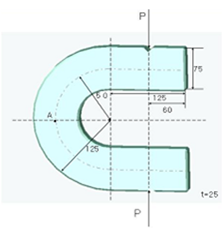
3. 곡선 보

	도심축

곡선보에 순수굽힘이 작용할 때 응력식은,

Winkler's fomula

이고, 여기서 A는 보의 단면적 M은 작용하는 모멘트 e는 중립축과 도심축 사이의 간극이 고 y는 중립축에서 측정지점까지의 거리이고 R은 다음과 같이 나타낼 수 있다.

실험 기구 및 장치

1. 실험 재료

스트레인게이지, SM-60D(Strain indicator), 인장시험기, 곡선보 등

실험 방법

1. 실험 과정

1) 미리 가공된 곡선 보의 표면을 사포 등을 이용하여 매끈하게 만들어 준다. 스트레인게이지를 곡선 보에 부착한다. 이때 기포가 발생하지 않도록 주의 한다.

 

2) 곡선 보를 인장시험기에 장착한다. 이때 MDS-2002 DATA ENCORDER의 zero 버튼을 눌러 영점을 잡는다.

 

3) 스트레인 게이지와 SM-60D(strain indicator)를 연결한다. 스트레인게이지의 리드 선을 SM-60D의 1과 2a에 연결하고 2a와 2를 연결하여 접지 한다.

 

4) Controller의 up&down 버튼을 눌러 하중을 100kgf부터 차례로 가한다.

 

5) SM-60D를 통해 변형률을 읽는다.

실험 결과

1. 결과 data

1) 곡선 보의 스트레인 게이지를 부착 시 변형률의 평균값

	스트레인 게이지를 바깥쪽에 부착	스트레인 게이지를 안쪽에 부착
초기값(0 kgf)	0	0
100 kgf	17.25	9.75
200 kgf	32.5	15
300 kgf	48	18.75
400 kgf	63.5	22.5
500 kgf	80.25	25.75

(변형률 10-6)

 

2) 곡선보의 스트레인 게이지를 부착 시 응력의 평균값

	스트레인 게이지를 바깥쪽에 부착	스트레인 게이지를 안쪽에 부착
초기값(0 kgf)	0	0
100 kgf	3.50175	1.97925
200 kgf	6.5975	3.045
300 kgf	9.744	3.80625
400 kgf	12.8905	4.5675
500 kgf	16.29075	5.22725

(단위: MPa, E: 203GPa)

 

2. 변형률과 응력의 그래프 선도 (평균값)

 

3. 해석 및 토론

1) 스트레인을 훅의 법칙 (σ=E·ε)에 적용하여 응력을 구한다.

하 중 (kgf)	100	200	300	400	500
σ=E·ε(MPa)	3.50175	6.5975	9.744	12.8905	s6.29075

 

2) 곡선보의 응력식 (Winkler's fomula) 을 이용해 분석적인 해를 구한다.

하 중 (kgf)	100	200	300	400	500
winkler's formula (MPa)	4.87	9.75	14.62	19.5	24.37

 

3) 직선보의 응력식 (σ=My/Iz)을 이용해 응력을 구하고 위의 두 값과 비교한다.

하 중 (kgf)	100	200	300	400	500
σ=My/Iz(MPa)	6.383	12.766	19.149	25.532	31.915

 

직선보와의 비교	100	200	300	400	500
훅의 법칙 차이 (%)	45.139	48.319	49.114	49.512	48.955
곡선보의 응력식 차이 (%)	23.703	23.625	23.651	23.625	23.640

4. 각 하중에 대한 응력 비교 그래프

토의 사항

1. 실험 고찰

본 실험은 스트레인 게이지를 부착한 곡선 보에 인장 시험기를 통해 하중을 가한 후 변형률을 측정하고, 그 수치를 이용하여 훅의 법칙에서 나온 실험상의 응력과 이론식인 직선보의 응력식과 곡선보의 응력식을 사용하여 나온 두 가지의 응력을 각기 비교 및 분석해보는 실험이었다. 차이를 나타낸 위의 결과에서 보면 알 수 있듯이 직선 보와의 비교에서 곡선 보 응력식으로 구한 응력보다 훅의 법칙을 이용하여 구한 응력에서 더 큰 오차가 발생하는 것을 볼 수 있다. 이러한 이유는 직선 보 응력 해석 방법으로 곡선 보를 해석하고 응력 계산을 하려다 보니 오차가 크게 발생한 것으로 볼 수 있다.

그리고 곡선 보에 하중이 작용할 때 곡선 보에 순수 굽힘뿐만 아니라 하중 P에 의해 발생 할 수 있는 압축 응력도 있을 것이며, 변형률 수치를 기록하면서도 변형률 수치가 계속적으로 약간씩 변하기 때문에 그 이상 자세할 수는 없었다. 그리고 곡선 보의 응력식을 이용하여 구한 응력과의 차이를 보면, 각 하중마다 거의 일정하게 차이를 보였음을 확인하였다.

본 실험을 통하여 곡선보의 응력식에서 계산한 응력이나 이나 훅의 법칙을 이용하여 나온 응력이나 둘 다 큰 차이를 발생시켰지만 곡선보의 응력식에서 나온 응력이 더 가까웠음을 확인하였다. 결과적으로 실험상의 값보다 이론상의 값이 더 일치하였다는 결론을 내릴 수 있었다.