실험 목적
확대-축소 또는 축소-확대 테이터 원관(tapered circular tube)속에 유체가 흐를 때, 베르누이 정리를 적용하여 압력수두, 속도수도, 위치수두와 관련된 유체의 에너지보전에 대해 실험으로 확인한다
실험 이론 및 원리
유체가 위의 그림과 같은 관 속을 흐를 때, 단위시간당 단면 ①에 유입하는 질량과 단면②를 통하여 유출한 질량의 차이는 관 속에 축적된 질량과 같다. 만약 정상류(Steady flow)이면, 질량보존의 법칙에 따라 유입되는 질량과 유출되는 질량은 같다. 이것을 연속방정식이라 한다.
2. 관련 식
m = ρ1A1V1 = ρ2A2V2
비압축성 유체 : ρ=일정 = ρ1 = ρ2
Q = A1V1 = A2V2
1) 에너지 보전법칙 (열역학 제 1법칙)
σQ - σW = σE
2) 비압축성 유체
3) 손실무시
실험 방법
① 밸브를 조정하여 물의 유량을 조정한다.
② 유량을 측정을 할 인원을 뽑아 시간을 정해 유량 측정한다.
③ 압력 수두를 읽을 인원을 뽑는다
④ 실험을 5번 하여 유량을 측정한다.
주의 사항
2. 압력수두를 잴 선이 꼬였을 때, 풀어 준 다음 실험에 임할 것.
실험 결과
d1=25㎜ d2=14.6㎜ d3=12.4㎜ | d4=11.3㎜ d5=10.6㎜ d6=10.0㎜ |
체적유량 Q=vol/t×1000(㎤/s) 평균속도 V=Q/A(㎝/s)
2. 실험 측정값
실험 횟수 | 측정값 | ||||||||
체적vol (ℓ) | 시간t (s) | 정압h1 [㎜Aq] | 정압h2 [㎜Aq] | 정압h3 [㎜Aq] | 정압h4 [㎜Aq] | 정압h5 [㎜Aq] | 정압h6 [㎜Aq] | 전압h7 [㎜Aq] | |
1 | 3.5 | 20.5 | 135 | 114 | 72 | 75 | 51 | 6 | 142 |
2 | 2.5 | 20 | 143 | 124 | 85 | 85 | 65 | 21 | 147 |
3 | 2.5 | 20 | 180 | 160 | 120 | 120 | 101 | 60 | 180 |
4 | 2.2 | 20 | 200 | 181 | 144 | 145 | 125 | 84 | 204 |
5 | 2.1 | 20 | 270 | 254 | 216 | 217 | 198 | 160 | 273 |
번호 | 관지름[㎜] | 넓이[㎟] |
tap 1 | 25 | 490.87385 |
tap 2 | 14.6 | 167.41547 |
tap 3 | 12.4 | 120.76282 |
tap 4 | 11.3 | 100.28749 |
tap 5 | 10.6 | 88.247338 |
tap 6 | 10 | 78.539816 |
3. 결과 분석
1) 각 위치의 속도
속도 (㎝/s) | 유량Q(㎤/s) | ||||
170.732(㎤/s) | 125 (㎤/s) | 125 (㎤/s) | 110 (㎤/s) | 105 (㎤/s) | |
tap 1 | 0.34781 | 0.25465 | 0.25465 | 0.22409 | 0.2139 |
tap 2 | 1.01981 | 0.74665 | 0.74665 | 0.65705 | 0.62718 |
tap 3 | 1.41378 | 1.03509 | 1.03509 | 0.91088 | 0.86947 |
tap 4 | 1.70242 | 1.24642 | 1.24642 | 1.09685 | 1.04699 |
tap 5 | 1.9347 | 1.41647 | 1.41647 | 1.2465 | 1.18984 |
tap 6 | 2.17382 | 1.59155 | 1.59155 | 1.40056 | 1.3369 |
2)속도 수두
속도 수두 [m] | |||||
tap 1 | 0.00593 | 0.003177 | 0.00318 | 0.00246 | 0.00224 |
tap 2 | 0.05096 | 0.027316 | 0.02732 | 0.02115 | 0.01927 |
tap 3 | 0.09794 | 0.052499 | 0.0525 | 0.04066 | 0.03704 |
tap 4 | 0.14201 | 0.076124 | 0.07612 | 0.05895 | 0.05371 |
tap 5 | 0.18341 | 0.098313 | 0.09831 | 0.07613 | 0.06937 |
tap 6 | 0.23155 | 0.124118 | 0.12412 | 0.09612 | 0.08758 |
3) 위치에 따른 전압
전압 | 실험횟수 | ||||
위치 | 1 | 2 | 3 | 4 | 5 |
tap 1 (㎝) | 14.0928 | 14.61774 | 18.3177 | 20.2461 | 27.2242 |
tap 2 (㎝) | 16.496 | 15.13165 | 18.7316 | 20.2154 | 27.3275 |
tap 3 (㎝) | 16.994 | 13.74988 | 17.2499 | 18.4655 | 25.3043 |
tap 4 (㎝) | 21.7014 | 16.11242 | 19.6124 | 20.3951 | 27.0713 |
tap 5 (㎝) | 23.4409 | 16.33134 | 19.9313 | 20.1134 | 26.737 |
tap 6 (㎝) | 23.755 | 14.51184 | 18.4118 | 18.0117 | 24.7578 |
토의 사항
본 실험에서 위치수두는 위치가 동일하기 때문에 생략이 가능하고, 연속방정식과 면적을 알고 있기에 손쉽게 속도를 구할 수 있었으며, 단면적이 클수록 속도는 작아지고, 단면적이 작으면 속도는 커진다는 것을 볼 수 있다. 그리고 유량에 따라 전체 압력이 달라진다는 것을 알 수 있었습니다.
베르누이 방정식으로 인하여 압력수두가 크면 속도 수두가 작아지며, 압력수두가 작으면 속도 수두가 커지는 것을 결과값으로 알 수 있습니다. 또한 전압은 압력수두와 속도수두의 합과 같다는 것을 처음 알게 되었습니다. 그러나 유체가 흐르면서 마찰로 인하여 손실수두가 생긴다는것을 알 수 있었습니다. 실험결과 중 전압이 다르게 나오는것을 보아 실험 중 잘못한 것이 있는것 같습니다.
본 실험으로 인하여 정압 을 이해하는데 도움이 되었으며, 아쉬운 점이 있다면, 눈으로 측정하여 눈금의 오차, 성급하게 실험을 하여 수주의 높이가 안정되지 않을 때 측정하거나 기계자체에서 오차가 발생 등 있어 다시 베르누이 방정식을 이해하는 시간이 되어 좋은 실험이 되었다.






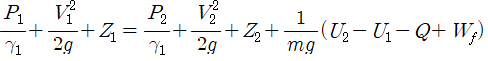





!&emoji=☕&slug=xFu35q9&button_colour=5F7FFF&font_colour=ffffff&font_family=Poppins&outline_colour=000000&coffee_colour=FFDD00)



![[일반생물학실험]온도와 pH가 효소작용에 미치는 영향 1부](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjdvNA5S925m8lScjFhJj-uy5SdCcaNFG1AuR_7BbQbDEoHBDEEkqfM64sipvro3RydmSO4_MS2794o2bJ0FCljQ31pcD5W39ZGOHROD7qKXLO1rlm2ZuBtbxJ9CZHSnsk2v1KSEsL4EGA/w680/%25EC%2598%25A8%25EB%258F%2584%25EC%2599%2580+pH%25EA%25B0%2580+%25ED%259A%25A8%25EC%2586%258C%25EC%259E%2591%25EC%259A%25A9%25EC%2597%2590+%25EB%25AF%25B8%25EC%25B9%2598%25EB%258A%2594+%25EC%2598%2581%25ED%2596%25A5.PNG)
![[일반생물학실험]여러 조건에 따른 효소 반응](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj4kaETe9N8j9q9-ClYy9V1kM2L9s5l19K6YoBOE0SB70BmssQXzVADvQijp1ieiQ9mIxcmCwz9e-YCQFVnXYR7m1vmfjTSs0ZNxCmBLG7wgzRBqiY1Kizx8YuhSdw-RDbs1PohokUd69c/w680/%25EC%2597%25AC%25EB%259F%25AC+%25EC%25A1%25B0%25EA%25B1%25B4%25EC%2597%2590+%25EB%2594%25B0%25EB%25A5%25B8+%25ED%259A%25A8%25EC%2586%258C+%25EB%25B0%2598%25EC%259D%2591.PNG)
![[일반생물학실험]항생제 감수성 검사 1부](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhwCJEjB_r2Ojsrn244q-fQmpHsDyUUfgWMUnsfhPKQeN2e7_u1pN_ZuwIdxPLVWS6LFywJUrDTYWJe2V6ZVVb1PtfyvX62Y15OxPfXoiaJkqVoSir3ZoFAmDpe5GcoMBmxEsJUKsSvWYc/w680/%25ED%2595%25AD%25EC%2583%259D%25EC%25A0%259C+%25EA%25B0%2590%25EC%2588%2598%25EC%2584%25B1+%25EA%25B2%2580%25EC%2582%25AC.PNG)
![[고분자공학실험]PMMA 중합 반응 - MMA, AIBN 정제와 PMMA Bulk 중합 1부](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj5hkRZhYWcXolP679_yO0kyP8_R-G9dlTqk5AGEdfsIq9M5K3DJc_tvpYck4x1kciBm2IWwFygrzfWH-HPzUjXiCHAFrjv9zeKYDxAl2tGNqgryyc3t9y4B9lQveS_coAqnmZw4pX4Hyo/w680/PMMA+%25EC%25A4%2591%25ED%2595%25A9+%25EB%25B0%2598%25EC%259D%2591.PNG)
![[일반화학실험]산화-환원 적정 : 비타민 C의 정량 1부](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEintFUW1pYHbKK8MPzki4vdqVMjTUEFFxPdZB1sTJQw13XSFZWqcN5w0x1AlyzfErlYYSgoNqBni4YGlpFC4ZeULK9VHbhfIXLiuZ3UWTl2oBRua7FE8UUQqtYEx3498FENAnlHlh0f8RFkT7Na8jveOtBtQ5UbY8jE80ZCwFoU_jqw_0Z6BofRYZF7/w680/%EC%82%B0%ED%99%94-%ED%99%98%EC%9B%90%20%EC%A0%81%EC%A0%95%20-%20%EB%B9%84%ED%83%80%EB%AF%BC%20C%EC%9D%98%20%EC%A0%95%EB%9F%89.PNG)
0 댓글