[일반화학실험]이산화탄소의 분자량 2부

실험 결과

1. 결과 분석

1) 실험의 외부조건

① 상온 : 17℃ (290 K)

② CO2 기체 플라스크의 온도 : 17℃ (290 K)

③ 기압: 1기압(가정)

④ 기체상수 R : 0.082 L·atm/㏖-1·K-1

⑤ 플라스크의 부피 : 132 ㎖(100㎖ 플라스크), 57㎖(50㎖ 플라스크)

⑥ 공기분자량 : 28.84 g ㏖-1

 

2) 공기에 의한 부력을 보정하기 위하여 플라스크에 들어있는 공기(78% 질소, 21% 산소, 1% 아르곤)의 무게를 계산한다.

공기의 분자량은 28.96g/㏖이고 실험실의 온도는 17℃로

따라서 T=290, 압력은 1기압, R=0.082

 

PV = nRT에서n = W / M이므로PV = (W/M)RT이다.

따라서 공기의 질량 W = PV·(M/RT)이다.

 

① 100㎖ - 플라스크의 총 부피 : 132(㎖)

플라스크 안의 공기의 질량 : W = PV·(M/RT) = 1 × 0.132 × 28.96 / (0.082 × 290) = 0.16 (g)

 

② 50㎖ – 플라스크의 총 부피 : 57(㎖)

플라스크 안의 공기의 질량 : W = PV·(M/RT) = 1 × 0.057 × 28.96 / (0.082 × 290) = 0.069(g)

 

3) 실험 결과로부터 플라스크에 들어있는 이산화탄소의 무게를 계산한다.

① 100㎖ – 순수한 플라스크와 유리판의 무게 : 79.52 – 0.16 = 79.36(g)

이산화탄소를 포함한 플라스크와 유리판의 무게 : 79.59(g)(1회), 79.60(g)(2회)

드라이아이스로 발생한 이산화탄소의 무게 : 0.23(g)(1회), 0.24(2회)

 

② 50㎖ – 순수한 플라스크와 유리판의 무게 : 58.19 – 0.069 = 58.12(g)

이산화탄소를 포함한 플라스크와 유리판의 무게 : 58.24(g)(1회, 2회)

드라이아이스로 발생한 이산화탄소의 무게 : 0.12(g)(1회, 2회)

4) 플라스크 부피의 이산화탄소의 무게와 공기의 무게의 비로부터 하여 이산화탄소의 분자량을 계산한다.

W(공기) : W(CO2) = PV·(M/RT)(공기) : PV·(M/RT)(CO2) = M(공기) : M(CO2)

M(CO2) = W(CO2)×(M(공기)/W(공기))

① 100㎖

(1회) M(CO2) = 0.23 × 28.96 / 0.16 = 41.63(g/㏖)

(2회) M(CO2) = 0.24 × 28.96 / 0.16 = 43.44(g/㏖)

M(평균) – (41.63 + 43.44) / 2 = 42.54(g/㏖)

 

② 50㎖ – (1회,2회)M(CO2)=0.12×28.96/0.069 = 50.29(g/㏖)

 

각각의 오차율은

이산화탄소 분자량의 이론값44.01(g/㏖)

① 100㎖의 경우 오차율 : {(42.54 - 44.01) / 44.01} × 100 = - 3.340%

② 50㎖의 경우 오차율 : {(50.29 - 44.01) / 44.01} × 100 = 14.27%

 

5) 실험 결과를 이상기체방정식, PV = (W/M)RT에 대입하여 이산화탄소의 분자량을 계산한다. 실내 압력은 1.0기압으로 가정한다. (R = 0.082 L·atm/㏖·K)

PV = nRT에서n = W / M을 대입하면PV = (W/M)RT

분자량 M = (W/PV)·RT

① 100㎖

(1회)M = 0.23 × (0.082 × 290) / (1 × 0.132) = 41.43(g/㏖)

(2회)M = 0.24 × (0.082 × 290) / (1 × 0.132) = 43.24(g/㏖)

M(평균) = (41.43 + 43.24) / 2 = 42.34(g/㏖)

 

① 50㎖ –(1회, 2회)

M = 0.12 × (0.082 × 290) / (1 × 0.057) = 50.06(g/㏖)

 

6) 유리판을 옮겼을 때 이산화탄소가 공기로 확산되어 나가면서 플라스크에 들어있는 혼합기체의 가상적인 분자량이 어떻게 변하는지 논한다.

유리판을 열어두게 되면 플라스크 안의 이산화탄소와 공기가 섞이게 된다. 이산화탄소보다 분자량이 가벼운 기체가 들어오게 되면서 상대적으로 무거운 이산화탄소는 줄어들게 되고 그로 인해 플라스크 안에 들어있던 이산화탄소량은 감소하게 되는 것이다.이산화탄소의 분자량이 공기보다 크기는 하지만 플라스크 내에서의 이산화탄소의 농도는 매우 높으므로 공기와의 혼합은 당연한 일이다. 공기의 평균 분자량은 이산화탄소의 분자량보다 작으므로 당연히 측정할 때 질량이 감소하게 된다.

 

 

토의 사항

1. 실험 고찰

실험1에서, 각각 무게비를 이용해서 구한 경우에100㎖ 플라스크에서 42.54(g/㏖), 50㎖ 플라스크에서 50.29(g/㏖)라는 분자량을, 이상기체방정식을 이용해서 구한 경우에는100㎖ 플라스크에서 42.34(g/㏖), 50㎖ 플라스크에서 50.06(g/㏖)라는 분자량을 구할 수 있었다. 100㎖ 플라스크에서 구한 값은 이산화탄소의 이론값인44.01(g/㏖)과 많이 차이가 났다.

 

특히 큰 플라스크에 비해서 작은 플라스크로 측정한 값은 오차가 훨씬 심했다. 적은 양을 측정했기 때문에 그만큼 정밀도가 떨어지는 것 같았다. 오차의 원인으로 몇 가지를 생각해 보았는데 그 중 물방울로 인한 오차는 없었을 거라고 추측해본다. 우리는 물방울이 생기지 않는 것을 직접 확인하면서 실험에 임했기 때문이다.

 

같은 압력, 같은 온도, 같은 부피에서라면 M=wRT/PV 라는 법칙에서 분자량이 질량과 온도에 비례하고 부피와 압력에 반비례한다는 것을 알아낼 수 있다. 우리가 직접 측정해 본 것은 부피, 온도, 그리고 스스로 계산해 본 질량인데, 이산화탄소 기체가 이상 기체의 성질을 따른다면 오차의 원인은 본래 양보다 적게 계산된 질량이나, 크게 측정된 부피라고 볼 수 있다.

 

측정기구로 인한 오차가 어느 정도 있었을 거라 생각하는데, 이를 측정오차 (measurement error)라고 한다. 50㎖부피 플라스크는A등급 기구일 경우에는 0.05정도, B등급 기구일 경우에는0.10정도의 오차가 생길 수 있다고 한다.

 

계산시의 유효숫자를 위한 반올림을 통해 버려지는 그 뒤의 값들로 인해 오차가 생겼을 수도 있다. 보다 정밀한 실험을 위해서는 반올림 없이 정확한 계산을 해야 하는 거겠지만 계산을 간략하게 하기 위해서 나는 유효숫자를 이용했다. 그 때 버려진 값들이 정밀도를 떨어트렸을 것이다.

 

또, 오차의 원인 중 하나로 이상 기체의 방정식을 사용한 점을 들 수 있다. 우리가 실험한 것은 실제 기체인데 그 실제 기체에 이상 기체 방정식을 적용함으로 인해 기체 입자들 사이의 인력과 기체 입자의 부피를 고려하지 못했다. 실제 기체에는 반데르발스 식(van der waals equation)을 사용할 수 있는데 이는 (P + (n2a/v2)) (V – nb) = nRT 의 식으로 나타낼 수 있다.

그러나 이보다 더 신뢰할 수 있는 방법으로 ‘비리얼 상태방정식’이 있다. 비리얼 상태방정식은 이상값1로부터Z(실제기체의 성질을 설명하는 데 유용한 양: 압축인자)의 편차를 이용하여 실험적인 상태방정식을 만든 것으로 그 식은 다음과 같이 표현할 수 있다.

Z = 1 + B/Vm + C/V2m + …

계수B,C,…는 비리알 계수(virial coefficient)라고 한다.

 

본 실험은 화학에서 사용하는 공식들을 실제로 실험해 볼 수 있는 좋은 기회를 가져다 주었다. 그저 책만 보고서 계산을 해보는 걸로 만족하지 않고 나아가서 어떻게 오차란 생겨나는가에 대해서도 알 수 있었다. 또 이론 값과 실제로 실험한 값의 오차 원인을 파악하는 것도 스스로 생각하게 함으로써 화학을 좀 더 이해하게 해 주는 데 도움이 되었다.

 

실험2에서는 실온 상태에서 기체로 승화되는 드라이아이스의 압력을 높이고 온도를 낮춤으로서 액체상태를 만들어 물방울을 관찰하는 것으로 이산화탄소의 삼중점을 알아보고자 했다.

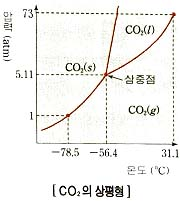
삼중점(Triple point)이란, 위의 상평형 그래프에서 볼 수 있듯이 고체, 액체 및 기체가 평형 상태로 공존하는 지점을 이른다.

 

위 그래프는 CO2의 상평형을 보여주는데, CO2 녹는점은 압력 증가에 따라 증가한다. 가 액체상태로 존재하려면 압력이5.2atm을 넘어야 하고 바로 이런 점을 이용해서 고체 (드라이 아이스)는 편리한 냉각제로 사용된다. 드라이아이스는 대기압 하에서 액체 상태의 중간 형태를 거치지 않고 직접 승화하기 때문이다. 따라서 아이스크림 보관 등에 사용이 가능하다.

 

인위적으로 드라이아이스를 타이곤 튜브에 넣고 완전히 밀봉하게 되면 승화작용이 일어나는데, 이 과정에서 당연히 압력이 증가하게 된다. 우리는 드라이아이스를 튜브에 넣고 실험을 했기 때문에 드라이아이스가 승화하면서 흡열 반응이 일어나 튜브 내의 온도가 무척 낮아지게 되었다. 그렇기 때문에 상당히 저온 상태에서 기체와 고체상의 평형곡선상에 도달하게 되는데, 이 상태는 주위와 온도 차가 커서 안정된 평형 상태가 아니다. 이 실험에서 드라이아이스는 튜브 밖으로부터 계속 열을 공급받아서 튜브 내에서는 고체-기체상 평형 곡선을 따라서 온도가 증가하는 방향으로 계속 비율이 변화하게 되고, 서서히 압력과 온도가 상승하게 된다. 이것이 계속 진행되면 삼중점에 이르게 되는 것이다.

 

실험에서 타이곤 튜브에 이산화탄소를 넣고 그것이 액화되는 과정을 지켜보기 위해 계속 기다렸다. 손으로 몇 번이고 타이곤 튜브를 문지르기도 했다. 하지만 꼼꼼히 살펴 보았음에도 불구하고 제대로 밀폐되지가 않았는지 직접 액체 이산화탄소를 보지는 못했다. 이 두 번째 실험을 위해서는 일단 무엇보다도 제대로 된 실험기구가 있어야 한다는 생각이 들었다. 

만일 하나 결함이 조금이라도 있는 경우, 실험을 할 수 없게 될 수도 있기 때문이다. 게다가 실험할 때에 터지는 소리가 주위에서 여럿 들려왔기 때문에 겁을 먹고 조금 느슨하게 니플을 조였다. 타이곤 튜브 안의 온도와 압력을 잴 수 없어 정확히 어떤 요인이 부족했는지는 모르지만 실험실 온도가 약17℃였다는 점을 생각했을 때 삼중점의 온도에 도달하는 것은 그리 어렵지 않기에 아무래도 압력이 부족했던 거라 추측한다.

 

2. 생각해볼 문제

1) 이상 기체 상태 방정식과 기체의 분자량을 구하는 식을 유도

PV = nRT 또는 PV = (W/M)·RT

구한 식을 통해 기체의 분자량 M=WRT/PV

 

2) 상온25℃에서1g의 드라이 아이스(CO2)가1기압(1 atm)의 기체로 전부 승화했을 경우, 그 부피 계산 과정을 쓰시오. (CO2 분자량=44, R=0.082 L·atm/K·㏖)

V = WRT/MP = (1g×0.082L·atm/K·㏖×298.15K)/(44g/㏖×1atm) = 0.556L

 

3) 아보가드로의 법칙을 설명하고, 공기와의 비교를 통한 이산화탄소 분자량 계산 과정을 이에 기초하여 설명하시오.

일정한 온도와 압력에서 기체의 부피는 그 몰수에 비례한다는 법칙이다. 이 때문에 실험에서 사용한 플라스크 내에 같은 양의 공기와 이산화탄소가 있다는 사실을 알 수 있고, 공기 및 이산화탄소의 무게의 비도 알 수 있기 때문에 공기의 분자량을 알면 이산화탄소의 분자량도 알 수 있다.

 

4) 100㎖ 삼각 플라스크에 들어간 드라이아이스의 양은 충분했는가? 과연1기압에서 필요한 드라이아이스의 부피는 얼마일까?

플라스크 안에 드라이아이스가 좀 더 필요했다는 생각이 든다. 이산화탄소의 분자량이44.01(g.㏖)로 나오기 위해서 필요한 드라이아이스의 질량은M = (W/PV)·RT라는 공식으로부터 W = (M/RT)·PV라는 공식을 생각해 내서 구해볼 수 있다. 계산 결과, W = 0.244g으로 나왔다. 

이로부터 필요한 드라이아이스의 부피를 구해보는데, 앞의 공식을 응용한V = WRT/MP로 계산해 보면V = 0.1318L 라는 값이 나온다. 1기압에서100㎖ 삼각 플라스크에 들어간 드라이 아이스의 양은 근소한 차이였지만 부족했고, 1기압에서 필요한100㎖ 삼각 플라스크 안의 드라이아이스의 부피는 0.1318L인 것을 알 수 있다.

 

5. 타이곤 튜브 안에서 액체 이산화탄소를 관찰하기 위해 필요한 드라이아이스의 양은? 그리고 그 안의 압력은 어느 정도여야 하는가? (지름, 길이 가정)

이론적으로 이산화탄소의 삼중점은 약 5.1 기압, -56.4℃ 지점에 있다. 이산화탄소가 삼중점이 되는 압력은 5.1atm 인데 5.1atm 이상의 압력이 있어야지만 이산화탄소가 액체상태로 존재할 수 있게 된다. 하지만 상온에서의 압력은 약1atm 정도이기 때문에 이산화탄소는 승화곡선에 따라 상태변화를 하게 되고 그에 따라 승화성을 띄게 된다.

이산화탄소의 온도는 드라이아이스의 온도로써 약-76°C이므로 우리가 한 실험에서 삼중점에 도달하게 하기 위해서 온도를 올리고 압력을 높이는 과정이 필요하다. 온도는 상온이 17°C 정도로 높기 때문에 드라이아이스를 이 온도에 노출시키는 것만으로도 저절로 올라간다. 또 테플론 테이프를 이용해서 튜브를 밀봉하고 이산화탄소가 승화되기를 기다리면 승화된 이산화탄소가 타이곤 튜브 안에 꽉 차면서 압력은 증가하게 된다.

 

타이곤 튜브의 지름이 2㎝이고, 길이가 20㎝라고 가정했을 경우, 타이곤 튜브의 부피는 62.8㎤이고 –56.4℃는 216.6K이다. W = MRT/PV 를 사용해서 필요한 드라이아이스의 양은 (44.01 × 0.082 × 216.6)/(5.1 × 62.8) = 2.440로 계산 된다. 압력을 구하기 위해서는P = MRT/WV 를 사용해야 하는데, (44.01 × 0.082 × 216.6)/(2.440 × 62.8) = 5.101로 계산된다. 따라서 지름이 2㎝이고, 길이가 20㎝인 타이곤 튜브 안에서 이산화탄소를 관찰하기 위해서는 2.440(g)의 드라이아이스가 필요하고 타이곤 튜브 안의 압력은 5.1atm 정도가 되어야 한다.

 

참고 문헌

1. 일반화학, MOORE STANITSKI JURS, 일반화학교재연구회, 자유아카데미, 2004, p.509-510

2. 최신 일반화학, 화학교재편찬연구회, 녹문당, 2004, p.324, p.368

3. 마스터톤의 일반화학, W. L. Masterton & C. N. Hurley, 화학교재연구회, 사이플러스, p.31

4. 핵심물리화학4thEdition, P. Atkins & J. D. Paul, 강춘형 외, 교보문고, 2006, p.34

5. 일반화학, Kenneth W. Whitten, 대학화학교재연구회, 삼경문화사, p.489

[Chemistry/일반화학] - [일반화학실험]이산화탄소의 분자량 1부