실험 결과
⑴ 인공위성의 운동 분석
인공위성의 초기상태를 알고 있는 상태에서 위성의 궤도를 분석하기 위해 모눈종이에 연필과 자를 이용하여 위성의 궤도를 작도했다. 위성의 위치를 13, 16단계로 표현하여 위성의 전체적인 궤도를 예측했다.
① 궤도 : 인공위성의 궤도를 그래프로 표시했다. rn값과 rn이 X축 = r0과 이루는 각도를 알면 쉽게 X좌표, Y좌표를 알 수 있고, 그래프로 표시할 수 있다.
② 각운동량/질량 : 각운동량은 l = mʋrsinθ 이다. 그런데 이 때, 인공위성의 질량은 주어진 정보가 없다. 인공위성 질량 m은 궤도를 도는 동안 일정한 상수이므로 l/m = ʋrsinθ의 값을 이용하여 각운동량이 보존되는지 확인할 수 있다. θ는 rn과 vn이 이루는 각도인데, 궤도를 도는 동안 θ는 항상 90°이다. 따라서, l/m = ʋr를 이용하여 각운동량 보존법칙을 확인해봤다.
③ 면적 : 면적 S = ½rnrn+1sinΦ(Φ=rn과 rn+1의 사잇각)을 이용하여 각 구간에서의 면적을 구할 수 있다. 이 면적들의 값은 모두 300초 동안 쓸고 지나간 면적 값이므로, 면적이 일정하면 면적속도가 일정하다는 것을 알 수 있다. 따라서, 면적 값을 구하여 면적속도 일정의 법칙을 확인해봤다.
⑵ 인공위성 B
인공위성 B의 초기조건은 r0 = 200 ㎜,= 65.0 ㎜이다.
실험은 r0부터 r13까지 그렸다.
① 궤도: 인공위성 B의 초기 궤도 반지름은 200㎜인데 시간이 지남에 따라 궤도 반지름이 점점 증가한다.
② 각운동량/질량: L/m을 이용하여 각운동량을 비교하였는데, 추세선의 식이 y = 0.831x + 43.54로 주어진다. 각운동량/질량의 평균은 48.53, 표준편차는 3.27이다.
③ 면적: 추세선의 식이 y = 21.21x + 6648로 주어진다. 면적의 평균은 6765.16, 표준편차는 184.36이다.
[분석] 인공위성 B는 반지름이 계속 큰 폭으로 증가하여 궤도가 포물선을 형성하며, 지구 반지름(143.5㎜)으로부터 멀어지는 것을 보아 탈출하리라는 것을 알 수 있다.
⑶ 인공위성 C
인공위성 C의 초기조건은 r0 = 200 ㎜,= 48.0 ㎜이다.
실험은 r0부터 r16까지 그렸다.
① 궤도: 인공위성 C의 반지름을 보면, 증가하는 경향이 계속 이어지다가 마지막에 감소하려는 경향을 보인다.
② 각운동량/질량: 위와 마찬가지로 L/m이용하여 각운동량을 비교하였는데, 추세선의 식이 y = -0.126x + 31.57으로 주어진다. 평균은 30.62, 표준편차는 0.72이다.
③ 면적: 면적 그래프의 추세선의 식은 y = -23.79x + 4749로 주어진다. 면적의 평균은 4583.07이고, 표준편차는 117.12이다.
[분석] 인공위성 C는 반지름이 증가하는 경향 중에 다시 감소하려는 경향을 보이므로, 타원 궤도를 그리고 있다.
2. 인공위성 A, B, C, D의 각운동량과 면적속도 분석
① 인공위성 B, C의 각운동량
각 위성의 각운동량/질량의 평균은 B에서 48.53, C에서 30.62를 갖는다. 그리고 표준편차는 각각 3.27, 0.72로 데이터들이 각각 비슷한 값을 가짐을 알 수 있다. 또한, 각각의 각운동량/질량의 그래프에서 추세선의 기울기가 각운동량/질량의 크기에 비해 매우 작으므로, 각운동량/질량이 거의 일정하게 보존된다고 할 수 있다.
질량은 일정한 상수이므로 각운동량이 거의 일정하게 보존된다는 것을 알 수 있다. 또한, B가 C보다 더 큰 값을 가짐을 볼 수 있는데, 그 이유는 B의 초기조건 가 C의
보다 크기 때문에, 더 큰 각운동량/질량 값을 가진다.
② 인공위성 B,C의 면적속도
각 위성이 300초 동안 쓸고 지나간 면적의 평균은 B는 6765.16, 표준편차는 184.36이고, C는 4583.07이고 표준편차는 117.12이다. 표준편차가 184.36, 117.12로 큰 값을 가지며, 면적의 변화 폭이 크다. 이는 위성의 궤도를 작도하면서 생긴 실험상 오차에서 비롯된 것이다. 그러나, 각각의 면적의 그래프에서 추세선의 기울기가 면적의 크기에 비해 매우 작으므로, 면적의 경향성이 거의 일정함을 알 수 있다.
따라서 면적이 정확이 어떤 특정한 값을 가지지는 못하지만, 이러한 경향성을 통해 물체가 300초 동안 쓸고 지나간 면적은 보존됨을 알 수 있고, 나아가 면적속도가 보존됨을 알 수 있다. 마찬가지로 B가 C보다 더 큰 면적 값을 가짐을 볼 수 있는데, 이 역시 초기조건이 C보다 B가 크기 때문이다.
3. 지구 상공 10km-원운동에 필요한 속도, 지표 탈출 필요 속도
지구 상공 10km에서 원운동을 하기 위해서는“구심력=지구의 중력”이라는 조건을 만족하므로, 지구의 반지름을 R, 인공위성의 상공 높이를 h, 지구의 질량을 M, 인공위성의 질량을 m이라 하면 다음과 같은 식을 만족한다.
이 식을 통해 ʋ를 구하면, 다음과 같다
R=6371㎞, h=10㎞에서 ʋ=7.91㎞/s 이다.
이제 지표 탈출에 필요한 속도를 생각해 보자. 지표를 탈출하려면, 지구반지름 R인 위치에서 위성의 운동에너지와 만유인력에 의한 위치에너지와의 합이 0 이상이면 탈출한다. 따라서, 다음과 같은 식을 만족하고, 탈출속도는 다음과 같이 쓸 수 있다.
여기서 R=6371㎞를 대입하면, ʋ > 11.2㎞/s 이면 탈출할 수 있다.
4. Scaling Factor의 유도
Scaling Factor는 다음과 식으로 나타낼 수 있다.
이 때, Δt=300s이고, G = 6.67259×10-11N·㎡/㎏2, M=5.9736×1024㎏이므로 상수값을 넣으면
마지막으로의 단위는 N·m3·㎏-1·s2이므로 1㎜ = 4.44×104m의 관계를 고려하면,

토의 사항
1. 오차의 원인
① 실제 계산값 만큼의 길이를 그릴 수 없었으며, 길이를 재는 과정에서도 애매한 경우가 다수 있었다. 실험에 사용한 자의 눈금이 완벽하게 정밀하지 못하고, 자 눈금을 읽어야 하는 사람의 측정에 있어서 한계가 있기 때문이다.
② ʋΔt의 평행을 맞추는 과정에서 오차가 발생했을 수 있다.
③ 300초 간격으로 직선운동을 그리고 그것을 합쳐 결과를 분석하였으나, 실제로 인공위성의 운동은 곡선운동이다.
2. 결론
본 실험은 실제로 한눈에 보기 힘들었던 인공위성의 운동을 일정한 비율로 줄인 후 인공위성의 초기 조건(위치, 속도)을 이용하여 지구의 주위를 궤도 운동하고 있는 인공위성의 전 궤도를 예측해보고, 각운동량 보존 법칙과 케플러 제 2법칙이 성립함을 확인하고, 탈출속도를 계산해보는 실험이였다.
결과적으로, 지구 궤도 상을 돌고 있는 인공위성은 그 반지름과 초기 속도에 따라 그 궤도가 원, 타원, 탈출(포물선, 쌍곡선) 또는 추락 궤도로 주어지며, 만유인력만이 작용할 때는 그 궤도에 관계없이 각운동량 보존 법칙과 면적 속도 일정 법칙이 성립한다.
사실상, 길이 측정 및 평행이동 등 실험 결과에 중요한 영향을 미치는 요소들이 모두 수작업으로 이루어진 데에서 많은 오차가 발생하였다. 인공위성의 초기 상태가 주어지면 위성의 궤적을 추적할 수 있는 프로그램이 있다면 매우 정확한 실험이 될 수 있을 것이고, 실험을 통해 확인한 각운동량 보존법칙과 케플러 제2법칙을 매우 작은 오차로 확인할 수 있을 것이다.
실험 시, 굉장히 많은 수작업을 요구하는 실험이라서 실험에 집중하기가 상당히 힘들었고, 따라서 더 많은 오차가 발생하게 되었다. 좀 더 인내심을 가지고 실험에 임하는 자세를 지녀야 할 것이다.
참고 문헌
Harris Benson, University Physics, p.313~317





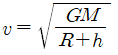




!&emoji=☕&slug=xFu35q9&button_colour=5F7FFF&font_colour=ffffff&font_family=Poppins&outline_colour=000000&coffee_colour=FFDD00)



![[일반생물학실험]온도와 pH가 효소작용에 미치는 영향 1부](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjdvNA5S925m8lScjFhJj-uy5SdCcaNFG1AuR_7BbQbDEoHBDEEkqfM64sipvro3RydmSO4_MS2794o2bJ0FCljQ31pcD5W39ZGOHROD7qKXLO1rlm2ZuBtbxJ9CZHSnsk2v1KSEsL4EGA/w680/%25EC%2598%25A8%25EB%258F%2584%25EC%2599%2580+pH%25EA%25B0%2580+%25ED%259A%25A8%25EC%2586%258C%25EC%259E%2591%25EC%259A%25A9%25EC%2597%2590+%25EB%25AF%25B8%25EC%25B9%2598%25EB%258A%2594+%25EC%2598%2581%25ED%2596%25A5.PNG)
![[일반생물학실험]여러 조건에 따른 효소 반응](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj4kaETe9N8j9q9-ClYy9V1kM2L9s5l19K6YoBOE0SB70BmssQXzVADvQijp1ieiQ9mIxcmCwz9e-YCQFVnXYR7m1vmfjTSs0ZNxCmBLG7wgzRBqiY1Kizx8YuhSdw-RDbs1PohokUd69c/w680/%25EC%2597%25AC%25EB%259F%25AC+%25EC%25A1%25B0%25EA%25B1%25B4%25EC%2597%2590+%25EB%2594%25B0%25EB%25A5%25B8+%25ED%259A%25A8%25EC%2586%258C+%25EB%25B0%2598%25EC%259D%2591.PNG)
![[일반생물학실험]항생제 감수성 검사 1부](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhwCJEjB_r2Ojsrn244q-fQmpHsDyUUfgWMUnsfhPKQeN2e7_u1pN_ZuwIdxPLVWS6LFywJUrDTYWJe2V6ZVVb1PtfyvX62Y15OxPfXoiaJkqVoSir3ZoFAmDpe5GcoMBmxEsJUKsSvWYc/w680/%25ED%2595%25AD%25EC%2583%259D%25EC%25A0%259C+%25EA%25B0%2590%25EC%2588%2598%25EC%2584%25B1+%25EA%25B2%2580%25EC%2582%25AC.PNG)
![[고분자공학실험]PMMA 중합 반응 - MMA, AIBN 정제와 PMMA Bulk 중합 1부](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj5hkRZhYWcXolP679_yO0kyP8_R-G9dlTqk5AGEdfsIq9M5K3DJc_tvpYck4x1kciBm2IWwFygrzfWH-HPzUjXiCHAFrjv9zeKYDxAl2tGNqgryyc3t9y4B9lQveS_coAqnmZw4pX4Hyo/w680/PMMA+%25EC%25A4%2591%25ED%2595%25A9+%25EB%25B0%2598%25EC%259D%2591.PNG)
![[일반화학실험]산화-환원 적정 : 비타민 C의 정량 1부](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEintFUW1pYHbKK8MPzki4vdqVMjTUEFFxPdZB1sTJQw13XSFZWqcN5w0x1AlyzfErlYYSgoNqBni4YGlpFC4ZeULK9VHbhfIXLiuZ3UWTl2oBRua7FE8UUQqtYEx3498FENAnlHlh0f8RFkT7Na8jveOtBtQ5UbY8jE80ZCwFoU_jqw_0Z6BofRYZF7/w680/%EC%82%B0%ED%99%94-%ED%99%98%EC%9B%90%20%EC%A0%81%EC%A0%95%20-%20%EB%B9%84%ED%83%80%EB%AF%BC%20C%EC%9D%98%20%EC%A0%95%EB%9F%89.PNG)
0 댓글