실험 결과
실험 시 사용한 에탄올 수용액(300㎖) 부피분율 10%수용액이다. 플라스크 전체의 무게는 421.70g으로 플라스크 무게 125.40g를 뺀 에탄올 수용액의 무게는 296.30g이다. 부피분율의 계산은 다음 식과 같다.
(9) |
부피분율에 밀도를 곱하면 질량분율로 바꿀 수 있다. 이때 혼합물의 밀도는 밀도 표를 참고한다.
(10) | |
(11) | |
(12) |
더 간단히 하기 위해 새로운 상수를 도입한다.
Table. 1. 에탄올 증류 실험
| 증류액 질량(g) | 누적 부피분율(%) | 순간 부피분율(%) |
1 | 8.97 | 66 | 61 |
2 | 9.13 | 59 | 57 |
3 | 9.28 | 52 | 46 |
4 | 9.50 | 40 | 20 |
5 | 9.79 | 17 | 11 |
6 | 9.87 | 10 | 5 |
7 | 9.94 | 4 | 3 |
8 | 9.97 | 2 | 1 |
(13) |
몰분율의 계산은 아래와 같다.
(14) |
위 식으로 구한 초기 수용액의 몰 분율은 0.03323이다. ne = 0.516㏖ 이고, nw = 15㏖ 이다. 증류실험을 통해 분리해 낸 에탄올 수용액의 실험값을 Table.1 에 정리했다.
Table. 2. 누적 농도에 대한 실험값 정리
| 에탄올 질량(g) | 에탄올 몰 수(㏖) | 물의 질량(g) | 물의 몰 수(㏖) | 에탄올 몰분율 (xe) |
1 | 5.219 | 0.113 | 3.751 | 0.208 | 0.353 |
2 | 4.665 | 0.101 | 4.465 | 0.248 | 0.290 |
3 | 4.112 | 0.0894 | 5.168 | 0.287 | 0.237 |
4 | 3.163 | 0.0688 | 6.337 | 0.352 | 0.163 |
5 | 1.344 | 0.0292 | 8.446 | 0.469 | 0.0586 |
6 | 0.791 | 0.0172 | 9.079 | 0.504 | 0.0330 |
7 | 0.316 | 0.00688 | 9.624 | 0.535 | 0.0127 |
8 | 0.158 | 0.00344 | 9.812 | 0.545 | 0.00627 |
에탄올의 총 몰수 ne는 0.516 ㏖이다. 여기서 에탄올의 몰 분율인 xF0을 구할 수 있다. xF0는 0.0332이다.
F1 = 15.0㏖ + 0.516㏖ = 15.516㏖
F1 = D1 + W1 | (15) |
두 번째 실험에서의 투입량은 첫 번째 실험증류 후 남은 양의 몰수와 같다.
F2 = W1 | (16) |
F2 = D2 + W2, F3 = W2 F3 = D3 + W3, F4 = W3 ∶ F8 = D8 + W8 | (17) |
위의 관계식을 통해 D와 W의 값을 구할 수 있다. Table. 2에 각 실험 회차의 누적 농도에 대한 실험값으로 구한 에탄올의 질량, 몰 수, 물의 질량과 몰 수, 그리고 에탄올의 몰분율 (xe) 값을 계산해 넣었다. 순간농도의 에탄올 몰 분율에서 우리가 구하고자 하는 기상의 에탄올 몰 분율(y*)를 구할 수 있다. 순간농도에 대한 실험값은 Table. 3에 정리해 놓았다. 이 값들로 구한 초기 몰 수(F), 증발하는 몰 수(D), 플라스크에 남은 몰 수(W)와, 그리고 각 몰 수에 대한 에탄올의 몰 분율(xF, xD, xW)을 Table. 4에 나타내었다.
Table. 3. 순간 농도에 대한 실험값 정리
| 에탄올 질량 (g) | 에탄올 몰 수 (㏖) | 물의 질량 (g) | 물의 몰 수 (㏖) | 에탄올 몰 분율 (y*) |
1 | 4.823 | 0.105 | 4.146 | 0.230 | 0.313 |
2 | 4.507 | 0.0980 | 4.623 | 0.257 | 0.276 |
3 | 3.637 | 0.0791 | 5.643 | 0.313 | 0.201 |
4 | 1.581 | 0.0344 | 7.918 | 0.440 | 0.0725 |
5 | 0.870 | 0.01891 | 8.920 | 0.496 | 0.0368 |
6 | 0.395 | 0.00860 | 9.475 | 0.526 | 0.0161 |
7 | 0.237 | 0.00516 | 9.703 | 0.539 | 0.00948 |
8 | 0.0791 | 0.00172 | 9.891 | 0.549 | 0.00312 |
Table. 4. F, D, W 값과 각 값에 대한 에탄올의 몰 분율
| F | D | W | xF | xD | xW | ln(F/W)i |
1 | 15.516 | 0.322 | 15.194 | 0.0333 | 0.353 | 0.0265 | 0.0210 |
2 | 15.194 | 0.350 | 14.845 | 0.0265 | 0.290 | 0.0203 | 0.0233 |
3 | 14.845 | 0.377 | 14.468 | 0.0203 | 0.237 | 0.0146 | 0.0257 |
4 | 14.468 | 0.421 | 14.0474 | 0.0146 | 0.163 | 0.0102 | 0.0295 |
5 | 14.047 | 0.498 | 13.549 | 0.0102 | 0.0586 | 0.00840 | 0.0361 |
6 | 13.549 | 0.522 | 13.0273 | 0.00840 | 0.0330 | 0.00741 | 0.0393 |
7 | 13.027 | 0.542 | 12.486 | 0.00741 | 0.0127 | 0.00718 | 0.0425 |
8 | 12.486 | 0.549 | 11.937 | 0.00718 | 0.00627 | 0.00723 | 0.0450 |
Table. 5. x, y*, 1/(y*-x)
| y* | x | 1/(y*-x) |
1 | 0.3128 | 0.0372 | 3.628 |
2 | 0.276 | 0.0316 | 4.0917 |
3 | 0.201 | 0.0234 | 5.631 |
4 | 0.0725 | 0.00651 | 15.154 |
5 | 0.0368 | 0.0036 | 30.120 |
6 | 0.0161 | 0.0016 | 68.966 |
7 | 0.00948 | 0.0009 | 116.550 |
8 | 0.00312 | 0.0005 | 381.680 |
Table. 5에는 순간 농도에 대한 에탄올의 기상 몰 분율 y*와 그 값에 대한 액상 몰 분율 x와 1/(y*-x)에 대해 나타내었다. 이 값은 에탄올 수용액의 Fig .7의 T-x,y그래프에서 구하였다. 여기서 구한 x와 1/(y*-x)에 대한 함수의 그래프를 Fig. 6에 나타내었다. 이 식을 x구간에 따라 적분하면 식(18)로 표현 된다. Rayleigh equation을 검증 하기 위해 Table. 4의 ln(F/W)i 값의 합을 구하면 ln(F/W)=0.262로 구해진다.
(18) |
오차(Error)의 계산은 아래의 식을 따른다.
(19) |
식 (19)에 100을 곱하면 %Error가 구해진다. 퍼센트 오차는 6.49%로 구할 수 있다.
토의 사항
1. 오차의 원인
첫째로 육안으로 관찰한 메스실린더의 값은 정확도가 떨어지기 때문이다. 부피분율 10%의 에탄올 수용액을 만들 때 부피를 정확하게 잴 수 없기 때문이다. 이러한 이유로 또한 에탄올 증류액의 값이 정확하지 않기 때문이다. 두 번째 이유는 증류 장치에서 접합점의 단열을 완벽하게 보장하지 못하기 때문이다. 실험당시 테프론이 없어서 플라스크와 증류장치가 만나는 부분에서 열이 새어 나갈 수 있는 공간이 만들어졌을 것이다. 여기서 발생하는 열 손실이 오차의 주요 원인이라 할 수 있다.
Fig. 9. x,1/(y*-x)의 그래프 | Fig. 10. T-x,y 그래프 |
2. 결론
서론에서 나타낸 분별증류의 원리에 대해 이해하고, 이를 이용해 에탄올 수용액의 단증류 실험을 시행하였다. 본 실험의 목적은 상평형 그래프의 이해와 이를 통해 Rayleigh equation의 검증이다. 실험값을 도입해 식을 검증한 결과 실험식과 이론식의 오차가 6.49%로, 오차의 원인으로는 다양한 원인이 있는데, 주 원인은 완전한 단열장치가 아님에 따라 발생하는 열 손실이라 생각된다.
3. 사용 기호
Ve : 에탄올의 부피 | Vw : 물의 부피 |
Vm : 혼합물의 부피 | me : 에탄올의 질량 |
mw : 물의 질량 | mm : 혼합물의 질량 |
ρe : 에탄올의 밀도 | ρw : 물의 밀도 |
ρm : 혼합물의 밀도 | ne : 에탄올의 몰수 |
nw : 물의 몰수 | nm : 혼합물의 몰수 |
Me : 에탄올의 분자량 | Mw : 물의 분자량 |
xe : 에탄올의 몰분율 | A : 에탄올 부피 분율 |




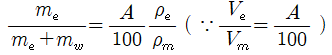







!&emoji=☕&slug=xFu35q9&button_colour=5F7FFF&font_colour=ffffff&font_family=Poppins&outline_colour=000000&coffee_colour=FFDD00)



![[일반생물학실험]온도와 pH가 효소작용에 미치는 영향 1부](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjdvNA5S925m8lScjFhJj-uy5SdCcaNFG1AuR_7BbQbDEoHBDEEkqfM64sipvro3RydmSO4_MS2794o2bJ0FCljQ31pcD5W39ZGOHROD7qKXLO1rlm2ZuBtbxJ9CZHSnsk2v1KSEsL4EGA/w680/%25EC%2598%25A8%25EB%258F%2584%25EC%2599%2580+pH%25EA%25B0%2580+%25ED%259A%25A8%25EC%2586%258C%25EC%259E%2591%25EC%259A%25A9%25EC%2597%2590+%25EB%25AF%25B8%25EC%25B9%2598%25EB%258A%2594+%25EC%2598%2581%25ED%2596%25A5.PNG)
![[일반생물학실험]여러 조건에 따른 효소 반응](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj4kaETe9N8j9q9-ClYy9V1kM2L9s5l19K6YoBOE0SB70BmssQXzVADvQijp1ieiQ9mIxcmCwz9e-YCQFVnXYR7m1vmfjTSs0ZNxCmBLG7wgzRBqiY1Kizx8YuhSdw-RDbs1PohokUd69c/w680/%25EC%2597%25AC%25EB%259F%25AC+%25EC%25A1%25B0%25EA%25B1%25B4%25EC%2597%2590+%25EB%2594%25B0%25EB%25A5%25B8+%25ED%259A%25A8%25EC%2586%258C+%25EB%25B0%2598%25EC%259D%2591.PNG)
![[일반생물학실험]항생제 감수성 검사 1부](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhwCJEjB_r2Ojsrn244q-fQmpHsDyUUfgWMUnsfhPKQeN2e7_u1pN_ZuwIdxPLVWS6LFywJUrDTYWJe2V6ZVVb1PtfyvX62Y15OxPfXoiaJkqVoSir3ZoFAmDpe5GcoMBmxEsJUKsSvWYc/w680/%25ED%2595%25AD%25EC%2583%259D%25EC%25A0%259C+%25EA%25B0%2590%25EC%2588%2598%25EC%2584%25B1+%25EA%25B2%2580%25EC%2582%25AC.PNG)
![[고분자공학실험]PMMA 중합 반응 - MMA, AIBN 정제와 PMMA Bulk 중합 1부](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj5hkRZhYWcXolP679_yO0kyP8_R-G9dlTqk5AGEdfsIq9M5K3DJc_tvpYck4x1kciBm2IWwFygrzfWH-HPzUjXiCHAFrjv9zeKYDxAl2tGNqgryyc3t9y4B9lQveS_coAqnmZw4pX4Hyo/w680/PMMA+%25EC%25A4%2591%25ED%2595%25A9+%25EB%25B0%2598%25EC%259D%2591.PNG)
![[일반화학실험]산화-환원 적정 : 비타민 C의 정량 1부](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEintFUW1pYHbKK8MPzki4vdqVMjTUEFFxPdZB1sTJQw13XSFZWqcN5w0x1AlyzfErlYYSgoNqBni4YGlpFC4ZeULK9VHbhfIXLiuZ3UWTl2oBRua7FE8UUQqtYEx3498FENAnlHlh0f8RFkT7Na8jveOtBtQ5UbY8jE80ZCwFoU_jqw_0Z6BofRYZF7/w680/%EC%82%B0%ED%99%94-%ED%99%98%EC%9B%90%20%EC%A0%81%EC%A0%95%20-%20%EB%B9%84%ED%83%80%EB%AF%BC%20C%EC%9D%98%20%EC%A0%95%EB%9F%89.PNG)
0 댓글