[효소]효소의 성질 3부






효소의 반응특성


효소의 촉매작용은 효소가 존재하지 않는 상태에 비해서 그 반응의 활성화에너지(ΔE)를 저하시킨다. 효소의 촉매작용에 기여하는 것으로 생각되는 다음과 같은 몇 가지의 인자가 활성화에너지를 저하시키는 것으로 생각되고 있다.

1) 기질의 접근과 유도 : 효소는 활성부위로 기질의 접근과 유도를 시도한다.


2) 기질구조의 변화 : 효소의 유도적합으로 활성부위의 구조가 변화되면 결합한 기질의 구조도 변화하게 된다.



3) 산 염기 촉매작용 : 효소의 활성부위는 아미노산 잔기의 치환기 R-로 되어 있으며 이들의 일반적인 산, 염기부분은 수계(水界)에서 대부분 유기화학반응의 강력한 촉매작용을 일으킨다.


4) 공유결합 촉매작용 : 효소는 기질과 불안정한 효소-기질 공유결합 중간체를 형성한다.

A → B라는 반응계의 반응경과에 대한 자유에너지 변화는 Fig. 2와 같다. 동일반응에서는 효소적이거나 비효소적이거나 Gibbs의 자유에너지 변화량(ΔG)과 평형상수는 변하지 않지만 활성화에너지는 변화한다. 일반적으로 화학반응 속도는 온도 상승과 함께 증가한다. 반응 속도상수 κ과 절대온도 T에 의한 변화는 Arrhenius 식으로 표현된다


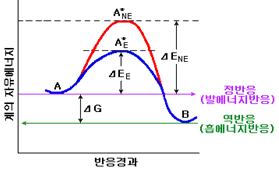Fig. 2 반응경과에 따른 계의 자유에너지의 변화

.A*NE = 비효소반응의 여기상태 또는 천이상태         A*E = 효소반응의 여기상태 또는 천이상태 

ΔENE = 비효소반응의 활성화에너지의 변화            ΔEE = 효소반응의 활성화에너지의 변화 

ΔG = 자유에너지의 변화

κ= Ae-E/RT(E = Arrhenius의 활성화에너지, A = 빈도인자)  ∴ ln κ = ln A - E/RT

즉 log κ = log A - E/2.303RT (R = 1.987 cal/mol·deg)로 된다. 이 식에서 온도가 10℃ 상승하면 반응속도는 약 2배로 된다고 알려져 있으며 경험적으로 비효소반응에 있어서 E는 10∼60 kcal/mol(37℃에서 15 kcal/mol 이상)을 나타내고 효소반응에서는 37℃에서 5∼15kcal/mol 정도이다.

Arrhenius식은 다음과 같이 나타낼 수도 있다.

d ln κ/dT = E/RT2   양변을 적분하면  ∫d ln κ = E/R ∫T -2 dT   ∴ ln κ = -E/RT + C

즉 κ= Ae-E/RT로 된다. 지금 23℃에서 반응 A → B의 비효소반응과 효소반응에 있어서 활성화에너지를 각각 ENE 15 및 EE 10kcal/mol이라면 logκE/κC = (15-10)/1.345 = 3.7이고 κE/κC = 103.7 ≒ 5,000이므로 효소반응속도는 비효소반응의 5,000배가 된다.


5) 온도의 영향

효소는 단백질이어서 온도가 일정 수준 이상으로 상승하면 단백질의 열변성이 일어나 활성효소가 감소하므로 반응속도는 낮아진다. 일반적으로 45℃까지는 온도의 상승과 함께 반응속도가 증가하지만 45℃를 넘으면 열변성이 시작되고 55℃ 이상이 되면 신속하게 변성을 일으켜 효소는 촉매로서의 기능을 잃게 된다. 그러므로 효소에는 최대 반응속도를 나타내는 온도(35∼45℃)가 있으며 이것을 최적온도(optimum temperature)라 한다.(Fig. 3 및 Fig. 4 참조)


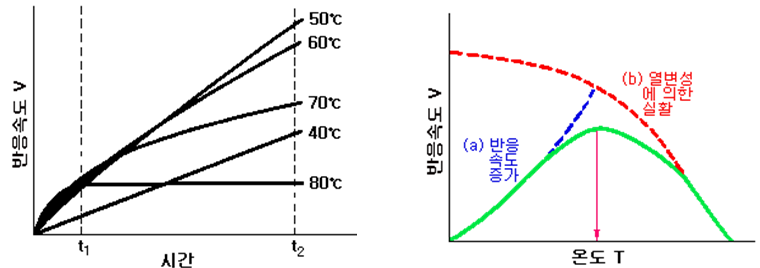Fig. 3 효소의 반응속도와 온도                  Fig. 4 효소의 반응최적온도

 

6) pH의 영향

효소는 한정된 범위의 pH에서만 활성이 있으며 이 범위내에서 효소의 안정성이 나타나고 반응속도가 최대로 되는 최적 pH(optimum pH)를 가진다. 양극단의 pH에서는 효소의 촉매부위가 파괴되기도 한다. 최적 pH에서는 효소 촉매부위의 proton 공여기 및 수용기, 효소-기질 복합체 그리고 기질이 적당한 이온화 상태로 되어 기질과의 친화성이 증가되므로 반응속도가 최대로 된다.


효소는 기질에 따라서 최적 pH가 변화하기도 하며 ATP, NAD+, 아미노산, coenzyme A 등과 같이 기질이 전해질인 경우에는 이들이 일정한 이온형이 아니면 효소는 작용하지 않는다. 세포내에서는 각 부위의 pH가 정확하게 유지되며 그 pH 조절기구는 세포의 대사조절과 밀접한 관계가 있다. 효소의 pH에 대한 상대반응속도를 그래프로 나타내면 종(鍾) 모양의 곡선(Fig. 5 참조)을 그리는 경우가 많으며 이런 형태의 pH 곡선은 활성부위에 2종류의 해리기가 있는 효소모델로 설명된다.


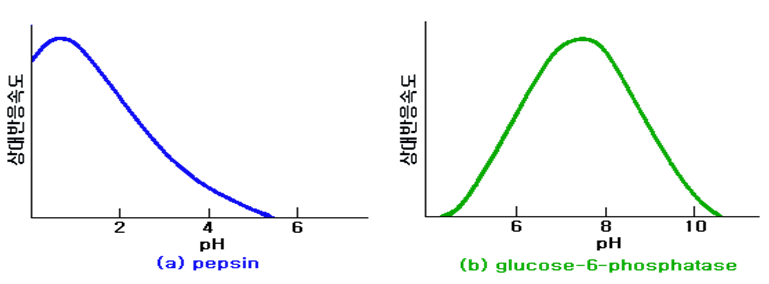Fig. 5 효소의 최적 pH







Reactions





댓글 쓰기

0 댓글